题目内容
8.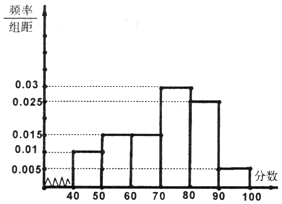 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:(1)求出物理成绩低于50分的学生人数;
(2)估计这次考试的平均分m与中位数n的值;
(3)设计一程序框图,根据输入的60名学生物理成绩输出这次考试的及格率.
分析 (1)由频率分布直方图求出物理成绩低于50分的学生所占频率与频数;
(2)由频率分布直方图计算这次考试的平均分与中位数即可;
(3)利用循环语句求出成绩大于或等于60分的人数,计算及格率即可.
解答 解:(1)由频率分布直方图得:
物理成绩低于50分的学生所占频率为:0.01×10=0.1,
∴物理成绩低于50分的学生人数为:0.1×60=6;
(2)估计这次考试的平均分:
m=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=70;
0.1+0.15+0.15=0.4<0.5,
∴中位数在[70,80)内,
则0.4+(n-70)×0.03=0.5,
解得中位数是n≈73.3;
(3)第一步:输入i=1,n=0;
第二步:输入成绩Xi(40≤Xi≤100),
判断Xi是否大于等于60,若是,则执行n=n+1,执行第三步;
否则,执行第三步;
第三步,i=i+1,判断i>60,若是,则计算并输出η=$\frac{n}{60}×100$%,程序结束;
否则,返回第二步.
点评 本题考查了频率分布直方图与平均数、中位数的应用问题,也考查了程序设计的问题,是综合题.

练习册系列答案
相关题目
16. 矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
 矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )| A. | $[0,\frac{π}{6}]$ | B. | $[0,\frac{π}{3}]$ | C. | $[0,\frac{π}{2}]$ | D. | $[0,\frac{2π}{3}]$ |
3.计算机执行如图的程序,输出的结果是( )


| A. | 1,3 | B. | 4,9 | C. | 4,8 | D. | 4,12 |
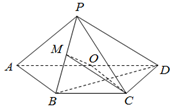 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.