题目内容
2.若一个扇形的弧长是3,半径是2,则该扇形的圆心角为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 6 | D. | 7 |
分析 由已知利用弧长公式即可计算得解.
解答 解:设扇形的弧长为l,圆心角大小为α(rad),半径为r,
由已知可得:l=3,r=2,
则由l=rα,可得:α=$\frac{l}{r}$=$\frac{3}{2}$.
故选:B.
点评 本题主要考查了弧长公式的应用,属于基础题.

练习册系列答案
相关题目
12.已知直线l在平面α内,则“l⊥β”是“α⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.在四面体S-ABC中,$AB⊥BC,AB=BC=\sqrt{2},SA=SC=2$,二面角S-AC-B的余弦值为$-\frac{{\sqrt{3}}}{3}$,则该四面体外接球的表面积是( )
| A. | $8\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 24π | D. | 6π |
14.下列函数中,既是奇函数又在定义域内单调递增的是( )
| A. | y=x3 | B. | y=tanx | C. | $y={(\frac{1}{2})^x}$ | D. | y=lnx |
11.设点A,B的坐标分别为(4,0),(-4,0),直线AP,BP相交于点P,且它们的斜率之积为实数m,关于点P的轨迹下列说法正确的是( )
| A. | 当m<-1时,轨迹为焦点在x轴上的椭圆(除与x轴的两个交点) | |
| B. | 当-1<m<0时,轨迹为焦点在y轴上的椭圆(除与y轴的两个交点) | |
| C. | 当m>0时,轨迹为焦点在x轴上的双曲线(除与x轴的两个交点) | |
| D. | 当0<m<1时,轨迹为焦点在y轴上的双曲线(除与y轴的两个交点) |
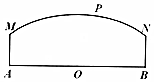 如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1.
如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1. 的前
的前 项和为
项和为 ,且
,且 ,数列
,数列 满足
满足
 ,
,
 的前
的前