题目内容
已知下列四个命题:
①若一个圆锥的底面半径缩小到原来的
,其体积缩小到原来的
;
②若两组数据的中位数相等,则它们的平均数也相等;
③直线x+y+1=0与圆x2+y2=
相切;
④“10a≥10b”是“lga≥lgb”的充分不必要条件;
⑤过M(2,0)的直线l与椭圆
+y2=1交于P1P2两点,线段P1P2中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-
.
其中真命题的序号是: .
①若一个圆锥的底面半径缩小到原来的
| 1 |
| 2 |
| 1 |
| 4 |
②若两组数据的中位数相等,则它们的平均数也相等;
③直线x+y+1=0与圆x2+y2=
| 1 |
| 2 |
④“10a≥10b”是“lga≥lgb”的充分不必要条件;
⑤过M(2,0)的直线l与椭圆
| x2 |
| 2 |
| 1 |
| 2 |
其中真命题的序号是:
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①一个圆锥的底面半径缩小到原来的
,则圆锥的底面积就缩小到原来的
,利用圆锥的体积公式,可得结论;
②若两组数据的中位数相等,根据平均数的计算公式,它们的平均数不一定相等;
③圆心到直线的距离为d=
=
,即可判断;
④“10a≥10b”,可以得出a≥b,不可以得出“lga≥lgb”,反过来,“lga≥lgb”,可得a≥b>0,∴“10a≥10b”;
⑤设点,代入椭圆方程,利用点差法,结合线段P1P2的中点为P,即可得到结论.
| 1 |
| 2 |
| 1 |
| 4 |
②若两组数据的中位数相等,根据平均数的计算公式,它们的平均数不一定相等;
③圆心到直线的距离为d=
| 1 | ||
|
| ||
| 2 |
④“10a≥10b”,可以得出a≥b,不可以得出“lga≥lgb”,反过来,“lga≥lgb”,可得a≥b>0,∴“10a≥10b”;
⑤设点,代入椭圆方程,利用点差法,结合线段P1P2的中点为P,即可得到结论.
解答:
解:①一个圆锥的底面半径缩小到原来的
,则圆锥的底面积就缩小到原来的
,又圆锥的体积=
×底面积×高,根据积的变化规律可得,体积缩小到原来的
,故①正确;
②若两组数据的中位数相等,根据平均数的计算公式,它们的平均数不一定相等,故②不正确;
③∵圆心到直线的距离为d=
=
,∴直线x+y+1=0与圆x2+y2=
相切,故③正确;
④“10a≥10b”,可以得出a≥b,不可以得出“lga≥lgb”,反过来,“lga≥lgb”,可得a≥b>0,∴“10a≥10b”,“10a≥10b”,是“lga≥lgb”的必要不充分条件;
⑤设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y,x12+2y12=2,x22+2y22=2,两式相减可得:(x1-x2)×2x+2(y1-y2)×2y=0,
∵直线l的斜率为k1(k1≠0),直线OP(O是原点)的斜率为k2,
∴k1k2=-
,正确.
故答案为:①③⑤.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
②若两组数据的中位数相等,根据平均数的计算公式,它们的平均数不一定相等,故②不正确;
③∵圆心到直线的距离为d=
| 1 | ||
|
| ||
| 2 |
| 1 |
| 2 |
④“10a≥10b”,可以得出a≥b,不可以得出“lga≥lgb”,反过来,“lga≥lgb”,可得a≥b>0,∴“10a≥10b”,“10a≥10b”,是“lga≥lgb”的必要不充分条件;
⑤设P1(x1,y1),P2(x2,y2),P(x,y),则x1+x2=2x,y1+y2=2y,x12+2y12=2,x22+2y22=2,两式相减可得:(x1-x2)×2x+2(y1-y2)×2y=0,
∵直线l的斜率为k1(k1≠0),直线OP(O是原点)的斜率为k2,
∴k1k2=-
| 1 |
| 2 |
故答案为:①③⑤.
点评:本题考查命题的真假判断,考查直线与圆的位置关系,考查直线与椭圆的位置关系,综合性强.

练习册系列答案
相关题目
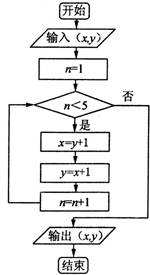
已知某算法的流程图如图所示,若输入x=7,y=6,则输出的有序数对为( )

| A、(13,14) |
| B、(12,13) |
| C、(14,13) |
| D、(13,12) |
设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |