题目内容
| ∫ | 2 1 |
| x2-2x-3 |
| x |
考点:定积分
专题:导数的综合应用
分析:利用定积分的运算法则,将所求化为和差的定积分,等于定积分的和与差.
解答:
解:原式=
(x-2-
)dx=(
x2-2x-3lnx)|
=-
-3ln2;
故答案为:-
-3ln2.
| ∫ | 2 1 |
| 3 |
| x |
| 1 |
| 2 |
2 1 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了定积分的计算;关键是利用定积分的运算法则解答.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
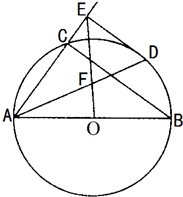 如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.
如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.