题目内容
已知{an}为等差数列，a2+a8=12，a4=5，令bn=a2n，判断数列{bn}是否为等差数列，若是，求其公差．
考点：等差关系的确定
专题：等差数列与等比数列
分析：由a2+a8=12求得a5，结合a4=5求出等差数列的首项和公差，求出通项公式，再由bn=a2n求得数列{bn}的通项公式，则可得数列{bn}是等差数列．
解答：
解：由于{an}为等差数列，可知a2+a8=2a5=12，得出a5=6，
又知a4=5，可求的公差d=a5-a4=6-5=1，
由此可知a1=a4-3d=5-3=2，
∴an=a1+（n-1）=2+n-1=n+1．
由此知bn=a2n=2n+1．
bn+1=2（n+1）+1=2n+3．
而bn+1-bn=2n+3-（2n+1）=2，
∴数列{bn}是等差数列．
又知a4=5，可求的公差d=a5-a4=6-5=1，
由此可知a1=a4-3d=5-3=2，
∴an=a1+（n-1）=2+n-1=n+1．
由此知bn=a2n=2n+1．
bn+1=2（n+1）+1=2n+3．
而bn+1-bn=2n+3-（2n+1）=2，
∴数列{bn}是等差数列．
点评：本题考查了等差数列的通项公式，考查了等差关系的确定，是基础题．
练习册系列答案
相关题目
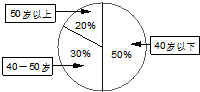某单位200名职工的年龄分布情况如图示，该单位为了解职工每天的睡眠情况，按年龄用分层抽样方法从中抽取40名职工进行调查．则应从40-50岁的职工中抽取的人数为（ ）
某中学从甲、乙两个艺术班中各选出7名学生参加市级才艺比赛，他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班学生成绩的众数是85，乙班学生成绩的中位数是83，则x+y的值为（ ）