题目内容
等比数列{an}中,a1=2,a4=16,
(1)若a3,a5分别是等差数列{bn}的第3项和第5项,求数列{bn}的通项公式;
(2)设cn=an+bn,求{cn}的前n项和Tn.
(1)若a3,a5分别是等差数列{bn}的第3项和第5项,求数列{bn}的通项公式;
(2)设cn=an+bn,求{cn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知求出等比数列的公比,进一步求出a3,a5,即等差数列{bn}的第3项和第5项,再求出等差数列的公差,然后代入等差数列的通项公式得答案;
(2)由(1)求出等比数列的通项公式,代入cn=an+bn,然后分别利用等比数列和等差数列的前n项和得
{cn}的前n项和Tn.
(2)由(1)求出等比数列的通项公式,代入cn=an+bn,然后分别利用等比数列和等差数列的前n项和得
{cn}的前n项和Tn.
解答:
解:(1)在等比数列{an}中,由a1=2,a4=16,
得q3=
=
=8,q=2.
∴a3=a1q2=8,a5=a1q4=32,
即b3=8,b5=32.
∵数列{bn}是等差数列,
∴d=
=
=12.
则bn=b3+(n-3)d=8+12(n-3)=12n-28;
(2)由(1)得,an=2n,bn=12n-28.
∴cn=an+bn=2n+12n-28.
∴{cn}的前n项和Tn=(a1+a2+…+an)+(b1+b2+…+bn)
=(2+22+…+2n)+(-16-4+8+…+12n-28)
=
+[-16n+
]=2n+1+6n2-22n-2.
得q3=
| a4 |
| a1 |
| 16 |
| 2 |
∴a3=a1q2=8,a5=a1q4=32,
即b3=8,b5=32.
∵数列{bn}是等差数列,
∴d=
| b5-b3 |
| 5-3 |
| 32-8 |
| 2 |
则bn=b3+(n-3)d=8+12(n-3)=12n-28;
(2)由(1)得,an=2n,bn=12n-28.
∴cn=an+bn=2n+12n-28.
∴{cn}的前n项和Tn=(a1+a2+…+an)+(b1+b2+…+bn)
=(2+22+…+2n)+(-16-4+8+…+12n-28)
=
| 2(1-2n) |
| 1-2 |
| 12n(n-1) |
| 2 |
点评:本题考查了等差数列和等比数列的通项公式,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
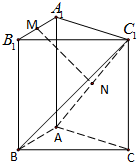 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.