题目内容
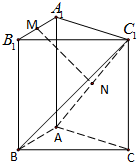 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.(1)求证:MN∥平面BCC1B1;
(2)求证:平面MAC1⊥平面ABC1.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)欲证MN||平面BCC1B1,根据直线与平面平行的判定定理可知只需证MN与平面BCC1B1内一直线平行即可,而连接BC1,AC1.根据中位线定理可知MN||BC1,又MN?平面BCC1B1满足定理所需条件;
(2)证明MN⊥BC1,MN⊥AC1,即可证明MN⊥平面ABC1,从而证明平面MAC1⊥平面ABC1.
(2)证明MN⊥BC1,MN⊥AC1,即可证明MN⊥平面ABC1,从而证明平面MAC1⊥平面ABC1.
解答:
 证明:(1)连接BC1,AC1.
证明:(1)连接BC1,AC1.
在△ABC1中,∵M,N是AB,A1C的中点,∴MN∥BC1.
又∵MN?平面BCC1B1,∴MN∥平面BCC1B1.
(2)∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形BCC1B1是正方形,
∴BC1⊥B1C,
∴MN⊥BC1,
连接AM,C1M,则△AMA1≌△B1MC1,
∴AM=C1M,
∵N是AC1的中点,
∴MN⊥AC1,
∵AC1∩BC1=C1,
∴MN⊥平面ABC1,
∵MN?平面MAC1,
∴平面MAC1⊥平面ABC1.
 证明:(1)连接BC1,AC1.
证明:(1)连接BC1,AC1.在△ABC1中,∵M,N是AB,A1C的中点,∴MN∥BC1.
又∵MN?平面BCC1B1,∴MN∥平面BCC1B1.
(2)∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形BCC1B1是正方形,
∴BC1⊥B1C,
∴MN⊥BC1,
连接AM,C1M,则△AMA1≌△B1MC1,
∴AM=C1M,
∵N是AC1的中点,
∴MN⊥AC1,
∵AC1∩BC1=C1,
∴MN⊥平面ABC1,
∵MN?平面MAC1,
∴平面MAC1⊥平面ABC1.
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒a∥β).

练习册系列答案
相关题目