题目内容
18.圆 C:(x-1)2+y 2=1 关于直线 l:x=0对称的圆的标准方程为(x+1)2+y2=1.分析 求出圆 C:(x-1)2+y 2=1的圆心为原点(1,0),半径为1,可得对称的圆半径为1,圆心为(-1,0),由此结合圆的标准方程即可得到所求圆的方程.
解答 解:∵圆 C:(x-1)2+y 2=1的圆心为原点(1,0),半径为1,
∴已知圆关于直线l:x=0对称的圆半径为1,圆心为(-1,0),
因此,所求圆的标准方程为(x+1)2+y2=1.
故答案为:(x+1)2+y2=1.
点评 本题给出圆 C:(x-1)2+y 2=1,求它关于定直线对称的圆的方程,着重考查了圆的标准方程、直线与圆的位置关系等知识,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
9.设集合U={-1,-2,-3,-4,0},集合A={-1,-2,0},集合B={-3,-4,0}则(∁UA)∩B=( )
| A. | {-3,-4} | B. | {-1,-2} | C. | {0} | D. | ∅ |
10.下列命题正确的是( )
| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线和两个相交平面都平行,则这两条直线与这两个平面的交线平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |
7.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 2π | B. | 4π | C. | 5π | D. | 6π |




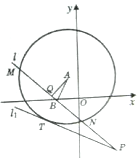 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.