题目内容
10.下列命题正确的是( )| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 若一条直线和两个相交平面都平行,则这两条直线与这两个平面的交线平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |
分析 利用直线与平面所成的角的定义,可排除A;利用面面平行的位置关系与点到平面的距离关系可排除B;利用线面平行的判定定理和性质定理可判断C正确;利用面面垂直的性质可排除D.
解答 解:对于A,若两条直线和同一个平面所成的角相等,则这两条直线的位置关系不能确定,故错;
对于B,若三个点共线,则这两个平面不一定平行,故错;
对于C,设平面α∩β=a,l∥α,l∥β,由线面平行的性质定理,在平面α内存在直线b∥l,在平面β内存在直线c∥l,所以由平行公理知b∥c,从而由线面平行的判定定理可证明b∥β,进而由线面平行的性质定理证明得b∥a,从而l∥a,故正确;
对于D,若两个平面都垂直于第三个平面,则这两个平面平行或相交,故错.
故选:C.
点评 本题主要考查了空间线面平行和垂直的位置关系,线面平行的判定和性质,面面垂直的性质和判定,空间想象能力,属基础题.

练习册系列答案
相关题目
20.在△ABC中,角A、B、C所对的边分别为a、b、c,已知$b=2,A=\frac{π}{3}$,且$\frac{c}{1-cosC}=\frac{b}{cosA}$,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$或$\sqrt{3}$ | D. | $\sqrt{3}$或$2\sqrt{3}$ |
1.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,则选中的花中没有红色的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{9}{10}$ |
2.下列关系正确的是( )
| A. | 0=∅ | B. | 1∈{1} | C. | ∅={0} | D. | 0⊆{0,1} |
20.数列$-\frac{1}{3}$,$\frac{1}{9}$,-$\frac{1}{27}$,$\frac{1}{81}$,…的一个通项公式可能是( )
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
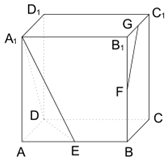 如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.
如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.