题目内容
13.已知直线C1:$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$( t 为参数),曲线C2:$\left\{\begin{array}{l}{x=rcosθ}\\{y=rsinθ}\end{array}\right.$(r>0,θ为参数).(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r=$\sqrt{2}$时,求点P 到直线C1距离最大时点P 的坐标.
分析 (1)参数方程化为普通方程,即可求C 1 与C2的交点坐标;
(2)利用圆的参数方程,结合点到直线的距离公式、三角函数公式,即可求点P 到直线C1距离最大时点P 的坐标.
解答 解:(1)直线C1:$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$( t 为参数)的普通方程为y=x-1,当r=1时,曲线C2:$\left\{\begin{array}{l}{x=rcosθ}\\{y=rsinθ}\end{array}\right.$(r>0,θ为参数)的普通方程为x2+y2=1.
联立方程,可得C 1 与C2的交点坐标为(1,0),(0,-1);
(2)设P($\sqrt{2}cosθ,\sqrt{2}sinθ$),则点P 到直线C1距离d=$\frac{|\sqrt{2}cosθ-\sqrt{2}sinθ-1|}{\sqrt{2}}$=$\frac{|2cos(θ+\frac{π}{4})-1|}{\sqrt{2}}$
当cos(θ+$\frac{π}{4}$)=-1,即θ=$\frac{3π}{4}$+2kπ(k∈Z)时,dmax=$\frac{3\sqrt{2}}{2}$,此时P(-1,1).
点评 本题考查参数方程化为普通方程,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
相关题目
3.已知映射f:A→B,其中A={x|x>0},B=R,对应法则f:x→-x2+2x,对于实数k∈B,在集合A中存在两个不同的原像,则k的取值范围为( )
| A. | k>0 | B. | k<1 | C. | 0<k≤1 | D. | 0<k<1 |
1.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,则选中的花中没有红色的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{9}{10}$ |
8.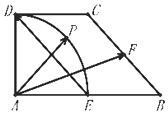 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分别为AB,AC 的中点,以A 为圆心,AD为半径的圆弧DE中点为P (如图所示).
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$,其中λ,μ∈R,则λ+μ的值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{4}$ |
2.下列关系正确的是( )
| A. | 0=∅ | B. | 1∈{1} | C. | ∅={0} | D. | 0⊆{0,1} |
 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,x≥0}\\{{a}^{x}-1,x<0}\end{array}\right.$,(x>0且a≠1)的图象经过点(-2,3).
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,x≥0}\\{{a}^{x}-1,x<0}\end{array}\right.$,(x>0且a≠1)的图象经过点(-2,3).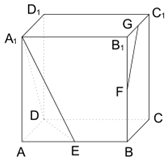 如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.
如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.