题目内容
以下四个命题中:
①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑用系统抽样,则分段的间隔k为30;
②直线y=kx与圆(x-cosθ)2+(y-sinθ)2=1恒有公共点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.15,则ξ在(2,3)内取值的概率为0.7;
④若双曲线
-y2=k的渐近线方程为y=±
x,则k=1.
其中正确命题的序号是 .
①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑用系统抽样,则分段的间隔k为30;
②直线y=kx与圆(x-cosθ)2+(y-sinθ)2=1恒有公共点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.15,则ξ在(2,3)内取值的概率为0.7;
④若双曲线
| x2 |
| 4 |
| 1 |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:阅读型
分析:由系统抽样的特点可判断①;②求出直线恒过的定点,代入圆的方程判断即可;根据正态分布的特点和曲线的几何意义即可判断③;根据双曲线方程与渐近线方程的关系即可判断④.
解答:
解:①由系统抽样的方法,将总体分成均衡的几部分,故分段的间隔k为
=20,故①错;
②直线y=kx恒过定点(0,0),而(0-cosθ)2+(0-sinθ)2=1,即直线与圆恒有一个交点,故②正确;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0),则曲线的对称轴为x=2,若ξ在(-∞,1)内取值的概率为0.15,则ξ在(3,+∞)内取值的概率为0.15,则ξ在(2,3)内与在(1,2)内的取值的概率相等均为0.35,故③错;
④若双曲线
-y2=k的渐近线方程为y=±
x,则若k>0,则a2=4k,b2=k,从而渐近线方程为y=±
x,若k<0,则易得渐近线方程为y=±
x,故k∈R且k≠0,故④错.
故答案为:②
| 600 |
| 30 |
②直线y=kx恒过定点(0,0),而(0-cosθ)2+(0-sinθ)2=1,即直线与圆恒有一个交点,故②正确;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0),则曲线的对称轴为x=2,若ξ在(-∞,1)内取值的概率为0.15,则ξ在(3,+∞)内取值的概率为0.15,则ξ在(2,3)内与在(1,2)内的取值的概率相等均为0.35,故③错;
④若双曲线
| x2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:②
点评:本题以命题的真假判断为载体,考查统计中的系统抽样的特点,直线与圆的位置关系和正态分布的特点以及双曲线方程与渐近线方程的关系,是一道基础题,必须掌握.

练习册系列答案
相关题目


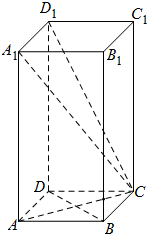 已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.
已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.