题目内容
集合A={-1，0，1}，B={y|y=x2+1，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{0，1} | D、{-1，0，1} |
考点：交集及其运算
专题：集合
分析：将A中的元素代入B中的等式变形求出y的值，确定出B，求出两集合的交集即可．
解答：
解：将A中的元素x=-1代入y=x2+1得：y=2；
将x=0代入y=x2+1得：y=1；
将x=1代入y=x2+1得：y=2，
∴B={1，2}，
则A∩B={1}．
故选：B．
将x=0代入y=x2+1得：y=1；
将x=1代入y=x2+1得：y=2，
∴B={1，2}，
则A∩B={1}．
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
下列函数中定义域为[1，+∞）的是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=(
| ||||
| D、y=ln（x-1） |
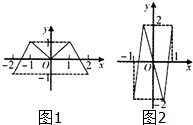如图，偶函数f（x）的图象形如字母M（图1），奇函数g（x）的图象形如字母N（图2），若方程f（g（x））=0．g（f（x））=0的实根个数分别为a，b，则a+b=（ ）| A、18 | B、21 | C、24 | D、27 |
已知边长为
的正方形ABCD的对角线BD上任意取一点P，则
•(
+
的取值范围是（ ）
| 2 |
| PB |
| PA |
| PC) |
| A、[0，1] | ||
B、[0，
| ||
| C、[-4，0] | ||
D、[-
|
关于直线l、m与平面α、β的命题中，一定正确的是（ ）
| A、若l∥m，m?α，则l∥α |
| B、若l⊥β，α⊥β，则l∥α |
| C、若l?β，α⊥β，则l⊥α |
| D、若l⊥β，α∥β，则l⊥α |
“a=-1”是“直线a2x-y+1=0与直线x-ay-2=0互相垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
命题p：“矩形的两条对角线相等”的逆命题是（ ）
| A、两条对角线相等的四边形是矩形 |
| B、矩形的两条对角线不相等 |
| C、有的矩形两条对角线不相等 |
| D、对角线不相等的四边形不是矩形 |