题目内容
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后关于y轴对称,则( )
| π |
| 2 |
| π |
| 3 |
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=4,φ=
| ||
D、ω=2,φ=-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:利用函数的周期求出ω,然后根据函数的平移法则求出函数的图象平移后的函数,然后由已知
的图象关于Y轴对称,求出φ,得到结果.
的图象关于Y轴对称,求出φ,得到结果.
解答:
解:由题意函数的周期是π,∴
=π,∴ω=2,
函数的图象向右平移
个单位后得到y=sin(2x-
+φ)的图象关于y轴对称,
∴-
+φ=kπ+
,k∈Z.∵|φ|<
,解得φ=
.
∴ω=2,φ=
.
故选:B.
| 2π |
| ω |
函数的图象向右平移
| π |
| 3 |
| 2π |
| 3 |
∴-
| 2π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
∴ω=2,φ=
| π |
| 6 |
故选:B.
点评:本题考查y=Asin(ωx+ϕ)的图象和性质,三角函数的左右平移一定要注意x上的变化量是解题中容易出错的地方,要引起注意,而函数的图象变换也是函数的重要知识,要熟练掌握.

练习册系列答案
相关题目
下列函数中定义域为[1,+∞)的是( )
A、y=
| ||||
B、y=
| ||||
C、y=(
| ||||
| D、y=ln(x-1) |
若a<b<0,那么下列不等式中正确的是( )
| A、ab<b2 | ||||
| B、ab>a2 | ||||
C、
| ||||
D、
|
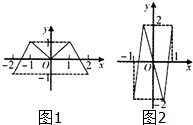 如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )
如图,偶函数f(x)的图象形如字母M(图1),奇函数g(x)的图象形如字母N(图2),若方程f(g(x))=0.g(f(x))=0的实根个数分别为a,b,则a+b=( )| A、18 | B、21 | C、24 | D、27 |
已知边长为
的正方形ABCD的对角线BD上任意取一点P,则
•(
+
的取值范围是( )
| 2 |
| PB |
| PA |
| PC) |
| A、[0,1] | ||
B、[0,
| ||
| C、[-4,0] | ||
D、[-
|
“a=-1”是“直线a2x-y+1=0与直线x-ay-2=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=(sinα,cos2α),
=(1-2sinα,-1),α∈(
,
),若
•
=-
,则tan(α-
)的值为( )
| a |
| b |
| π |
| 2 |
| 3π |
| 2 |
| a |
| b |
| 8 |
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|