题目内容
已知函数f(x)=lnx-
(Ⅰ)求证:f(x)在区间(0,+∞)上单调递增;
(Ⅱ)若f[x(3x-2)]<-
,求实数x的取值范围.
| x |
| 1+2x |
(Ⅰ)求证:f(x)在区间(0,+∞)上单调递增;
(Ⅱ)若f[x(3x-2)]<-
| 1 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求导数即可;
(Ⅱ)将-
写成f(1),再根据(Ⅰ)即可利用函数的单调性求得实数x的取值范围.
(Ⅱ)将-
| 1 |
| 3 |
解答:
(Ⅰ)证明:由已知得f(x)的定义域为(0,+∞)
∵函数f(x)=lnx-
,
∴f′(x)=
-
=
.
∵x>0,
∴4x2+3x+1>0,x(1+2x)2>0.
∴当x>0时,f′(x)>0.
即f(x)在区间(0,+∞)上单调递增;
(Ⅱ)∵函数f(x)=lnx-
,
∴f(1)=ln1
=-
.
由f[x(3x-2)]<-
可得
f[x(3x-2)]<f(1).
由(Ⅰ)得
,
解得-
<x<0或
<x<1.
故实数x的取值范围为(-
,0)∪(
,1).
∵函数f(x)=lnx-
| x |
| 1+2x |
∴f′(x)=
| 1 |
| x |
| 1+2x-2x |
| (1+2x)2 |
| 4x2+3x+1 |
| x(1+2x)2 |
∵x>0,
∴4x2+3x+1>0,x(1+2x)2>0.
∴当x>0时,f′(x)>0.
即f(x)在区间(0,+∞)上单调递增;
(Ⅱ)∵函数f(x)=lnx-
| x |
| 1+2x |
∴f(1)=ln1
| 1 |
| 1+2×1 |
| 1 |
| 3 |
由f[x(3x-2)]<-
| 1 |
| 3 |
f[x(3x-2)]<f(1).
由(Ⅰ)得
|
解得-
| 1 |
| 3 |
| 2 |
| 3 |
故实数x的取值范围为(-
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查利用求导的方法判断函数的单调性以及求满足条件的自变量的区间.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=
sin(ωx+φ+
)对任意的实数x,有f(-x)=f(x),则tanφ的值为( )
| 2 |
| π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
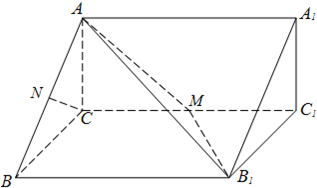 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1上的一点.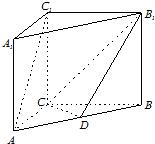 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.