题目内容
二次函数的图象与x轴的两个交点(-2,0),(4,0),且过点(1,9),则解析式为 .
考点:二次函数的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:先设出函数的表达式,将(1,9)代入表达式,求出a的值即可.
解答:
解:∵二次函数的图象与x轴的两个交点是(-2,0),(4,0),
∴设函数的解析式为y=a(x+2)(x-4),
将(1,9)代入y=a(x+2)(x-4),
得:a=-1,
∴y=-x2+2x+6,
故答案为:y=-x2+2x+6.
∴设函数的解析式为y=a(x+2)(x-4),
将(1,9)代入y=a(x+2)(x-4),
得:a=-1,
∴y=-x2+2x+6,
故答案为:y=-x2+2x+6.
点评:本题考查了求二次函数的解析式问题,本题属于基础题.

练习册系列答案
相关题目
若连续抛两次骰子分别所得的点数a,b作为点P的横、纵坐标,则点P在直线x+y=5下方的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
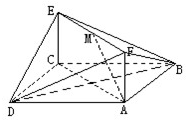 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: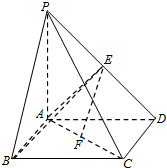 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.