题目内容
若方程
+
=1,a∈[1,5],b∈[2,4]表示焦点在x轴上且离心率小于
的椭圆,则z=a+b的最小值为 .
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:计算题,不等式的解法及应用
分析:表示焦点在x轴上且离心率小于
的椭圆时,可得
,利用线性规划知识,即可求出z=a+b的最小值.
| ||
| 2 |
|
解答:
 解:方程方程
解:方程方程
+
=1,表示焦点在x轴上且离心率小于
的椭圆时,
有
,化简得
,
又a∈[1,5],b∈[2,4],画出满足不等式组的平面区域,如右图阴影部分所示,
令z=y+x,平移直线y=-x+z,当过(2,2)时,zmin=4.
故答案为:4.
 解:方程方程
解:方程方程| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
有
|
|
又a∈[1,5],b∈[2,4],画出满足不等式组的平面区域,如右图阴影部分所示,
令z=y+x,平移直线y=-x+z,当过(2,2)时,zmin=4.
故答案为:4.
点评:本题考查椭圆的简单性质,考查线性规划知识,比较基础.

练习册系列答案
相关题目
若θ为三角形中最大内角,则直线l:xtanθ+y+m=0的倾斜角的范围是( )
A、(0,
| ||||||||
B、(
| ||||||||
C、(0,
| ||||||||
D、(0,
|
设集合M={x|x2-2x-3<0},N={x|log2(x-1)≤1},则M∩N等于( )
| A、{x|-1<x<3} |
| B、{x|1<x≤3} |
| C、{x|1<x<3} |
| D、{x|-1≤x≤3} |
已知f(
+1)=x+2
,则f(x)的解析式为( )
| x |
| x |
| A、x2-1 |
| B、x2+1 |
| C、x2+x+1 |
| D、x2-1(x≥1) |
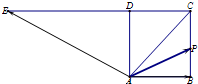 如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,
如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD.动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,