题目内容
20.求圆心在直线x+y=0上,且过直线x-2y+4=0与圆x2+y2+2x+2y-8=0的交点的圆的方程.分析 先求得直线x-2y+4=0与圆x2+y2+2x+2y-8=0的交点,设所求圆心坐标为(a,-a),则(a,-a)到两圆交点(-4,0)和(0,2)的距离相等,求得a的值,可得圆心和半径,从而求得要求的圆的方程.
解答 解:将直线与圆的方程联立得方程组$\left\{{\begin{array}{l}{x-2y+4=0}\\{{x^2}+{y^2}+2x+4y-8=0}\end{array}}\right.$,消去x得到y2-2y=0,解得:y=0或y=2,
两圆的交点坐标A(-4,0),B(0,2).
因所求圆心在直线x+y=0上,故设所求圆心坐标为(a,-a),则(a,-a)到两圆交点(-4,0)和(0,2)的距离相等,
故有:$\sqrt{{(a+4)}^{2}{+(-a)}^{2}}$=$\sqrt{{(a-0)}^{2}{+(-a-2)}^{2}}$,
即4a=-12,∴a=-3,从而圆心坐标是(-3,3),
又$r=\sqrt{{{(-4+3)}^2}+{3^2}}=\sqrt{10}$,故所求圆的方程为(x+3)2+(y-3)2=10.
点评 本题主要考查求两曲线的交点,求圆的标准方程,求出圆心和半径,是解题的关键,属于基础题.

练习册系列答案
相关题目
15.过点P(2,3)并且在两坐标轴上截距相等的直线方程为( )
| A. | 2x-3y=0 | B. | 3x-2y=0或x+y-5=0 | ||
| C. | x+y-5=0 | D. | 2x-3y=0或x+y-5=0 |
10.已知命题P的逆命题是“若a、b都不是偶数,则ab不是偶数”,则命题P的逆否命题是( )
| A. | 若a、b都是偶数,则ab是偶数 | |
| B. | 若ab是偶数,则a、b都是偶数 | |
| C. | 若a、b至少有一个是偶数,则ab是偶数 | |
| D. | 若ab是偶数,则a、b至少有一个是偶数 |
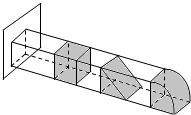 如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.
如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.