题目内容
3.数列{an}满足:a1=-9,an+1-an=2,Sn是其前n项和,则S10=( )| A. | 0 | B. | -9 | C. | 10 | D. | -10 |
分析 通过条件可确定该数列为等差数列,进而利用公式计算即得即可.
解答 解:∵a1=-9,an+1-an=2,
∴数列{an}是首项为-9,公差为2的等差数列,
∴S10=-9×10+$\frac{10×(10-1)}{2}$×2=0,
故选:A.
点评 本题考查等差数列的判定,考查等差数列的求和公式,注意解题方法的积累,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.若x,y满足约束条件$\left\{{\begin{array}{l}{x-y≤0}\\{2x-y≥0}\\{2x+y≤4}\end{array}}\right.$,z=x+y+3与z=x+ny取得最大值的最优解相同,则实数n的取值范围是( )
| A. | {1} | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | [1,+∞) |
18.已知命题“?x∈R,ax2+4x+1>0”是假命题,则实数a的取值范围是( )
| A. | (4,+∞) | B. | (0,4] | C. | (-∞,4] | D. | [0.4) |
8.已知函数g(x)的导函数g'(x)=ex,且g(0)g'(1)=e,(其中e为自然对数的底数).若?x∈(0,+∞),使得不等式$g(x)<\frac{x-m+3}{{\sqrt{x}}}$成立,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
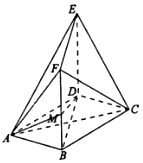 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.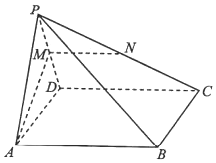 如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证: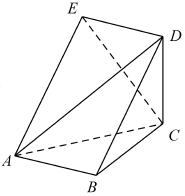 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.