题目内容
11.设x0为函数f(x)=sinπx的零点,且满足|x0|+|f(x0+$\frac{1}{2}$)|<33,则这样的零点有( )| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
分析 令f(x0)=0得x0=k,由f(x)的周期为2可得f(x0+$\frac{1}{2}$)=±1,代入条件式得|k|<32.
解答 解:f(x)的周期T=$\frac{2π}{π}$=2,∵设x0为函数f(x)=sinπx的零点,∴x0=k(k∈Z),f(x0)=0,∴|f(x0+$\frac{1}{2}$)|=1,
∴|k|<32.∴符合条件的k共有63个.
故选B.
点评 本题考查了正弦函数的性质,零点的定义,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.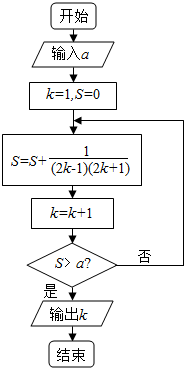 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
6.在数列{an}中,若a1=2,且对任意正整数m、k,总有am+k=am+ak,则{an}的前n项和为Sn=( )
| A. | n(3n-1) | B. | $\frac{n(n+3)}{2}$ | C. | n(n+1) | D. | $\frac{n(3n+1)}{2}$ |
16.已知数列{an}的各项均为正数,a1=2,an+1-an=$\frac{4}{{a}_{n+1}+{a}_{n}}$,若数列{$\frac{1}{{a}_{n+1}+{a}_{n}}$}的前n项和为5,则n=( )
| A. | 35 | B. | 36 | C. | 120 | D. | 121 |
3.已知函数y=f(x)在区间[1,2]上单调递增,且满足f(1)-f(2)<0,则f(x)在(1,2)上( )
| A. | 有一个零点 | B. | 有两个零点 | C. | 可能没有零点 | D. | 以上说法不正确 |
 如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角.
如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角. 如图,一辆汽车在一条水平的公路上向正西行驶,在A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,求此山的高度CD.
如图,一辆汽车在一条水平的公路上向正西行驶,在A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,求此山的高度CD.