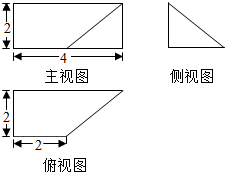
题目内容
1. 如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角.
如图,单位圆⊙O与x轴正半轴交于点A,角α与β的终边分别与单位圆交于B(xB,yB)、C(xC,yC)两点,且满β-α=$\frac{π}{4}$,其中α为锐角.(1)当△AOB为正三角形时,求$\overrightarrow{OC}$•$\overrightarrow{AB}$;
(2)当xC=-$\frac{3}{5}$时,求S△AOB.
分析 (1)α=$\frac{π}{3}$,β=$\frac{π}{3}+\frac{π}{4}$=$\frac{7π}{12}$,求出A,B,C的坐标,写出$\overrightarrow{OC},\overrightarrow{AB}$的坐标,代入数量积公式计算;
(2)cosβ=-$\frac{3}{5}$,sinβ=$\frac{4}{5}$,利用差角公式计算出sinα,代入面积公式即可求出面积.
解答 解:(1)当△AOB为正三角形时,α=$\frac{π}{3}$,β=$\frac{π}{3}+\frac{π}{4}$=$\frac{7π}{12}$,
∴B($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),C($\frac{\sqrt{2}-\sqrt{6}}{4}$,$\frac{\sqrt{2}+\sqrt{6}}{4}$),A(1,0).
∴$\overrightarrow{AB}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{OC}$=($\frac{\sqrt{2}-\sqrt{6}}{4}$,$\frac{\sqrt{2}+\sqrt{6}}{4}$),
∴$\overrightarrow{OC}•\overrightarrow{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{8}$+$\frac{\sqrt{6}+3\sqrt{2}}{8}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
(2)∵xC=cosβ=-$\frac{3}{5}$,∴sinβ=$\frac{4}{5}$,
∴sinα=sin($β-\frac{π}{4}$)=sinβcos$\frac{π}{4}$-cosβsin$\frac{π}{4}$=$\frac{7\sqrt{2}}{10}$.
∴S△AOB=$\frac{1}{2}$OA•OBsinα=$\frac{7\sqrt{2}}{20}$.
点评 本题考查了平面向量的数量积运算,三角函数求值,属于基础题.

| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
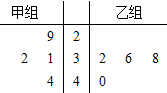 某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.
某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.