题目内容
8.曲线C:y=ex同曲线C在x=0处的切线及直线x=2所围成的封闭图形的面积为( )| A. | e+1 | B. | e-1 | C. | e2-1 | D. | e2-5 |
分析 求出函数的导数,可得切线的斜率和切点,由斜截式方程可得切线的方程,分别作出曲线和切线及x=2,得到封闭图形.再由定积分${∫}_{0}^{2}$(ex-x-1)dx,计算即可得到所求面积.
解答 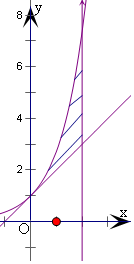 解:y=ex的导数为y′=ex,
解:y=ex的导数为y′=ex,
可得在x=0处的切线斜率为k=1,
切点为(0,1),可得切线的方程为y=x+1,
分别作出曲线和切线及x=2,得到如图的封闭图形.
则封闭图形的面积为${∫}_{0}^{2}$(ex-x-1)dx=(ex-$\frac{1}{2}$x2-x)|${\;}_{0}^{2}$
=(e2-2-2)-(e0-0-0)=e2-5.
故选:D.
点评 本题考查导数的运用:求切线的方程,考查不规则图形的面积的求法,注意运用定积分计算,考查运算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.已知cosθ=-$\frac{3}{5}$($\frac{π}{2}$<θ<π),则cos($θ-\frac{π}{3}$)=( )
| A. | $\frac{4\sqrt{3}+3}{10}$ | B. | $\frac{4\sqrt{3}-3}{10}$ | C. | -$\frac{4\sqrt{3}+3}{10}$ | D. | $\frac{4-3\sqrt{3}}{10}$ |
19.若函数f(x)=|x2-4x|-a有4个零点,则实数a的取值范围是( )
| A. | (0,2) | B. | (-∞,-4) | C. | (4,+∞) | D. | (0,4) |
3.已知i为虚数单位,复数z满足$z+zi=|\sqrt{3}-i|$,则复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.7个人排成一队参观某项目,其中ABC三人进入展厅的次序必须是先B再A后C,则不同的列队方式有多少种( )
| A. | 120 | B. | 240 | C. | 420 | D. | 840 |