题目内容
12．已知三条直线a、b、c两两平行且不共面，这三条直线可以确定m个平面，这m个平面把空间分成n个部分，则（ ）| A． | m=2 n=2 | B． | m=2 n=6 | C． | m=3 n=7 | D． | m=3 n=8 |
分析 利用推论三能求出m的值，再利用平面的基本性质及推论能求出n的值．
解答 解：根据推论3（经过两条平行直线有且只有一个平面）知三条直线a、b、c两两平行但不共面时，
这三条直线可以确定3个平面，即m=3．
三条直线把平面分成七个部分．
如把直线看成平面，则三个平面把空间也分成了七个部分，即n=7．
故选：C．
点评 本题考查平面的基本性质及推论的应用，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
相关题目
14．
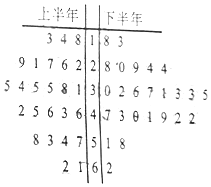自贡某工厂于2016年下半年对生产工艺进行了改造（每半年为一个生产周期），从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示（如图）．已知每个生产周期内与其中位数误差在±5范围内（含±5）的产品为优质品，与中位数误差在±15范围内（含±15）的产品为合格品（不包括优质品），与中位数误差超过±15的产品为次品．企业生产一件优质品可获利润20元，生产一件合格品可获利润10元，生产一件次品要亏损10元
（Ⅰ）求该企业2016年一年生产一件产品的利润为10的概率；
（Ⅱ）是否有95%的把握认为“优质品与生产工艺改造有关”．
附：
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
自贡某工厂于2016年下半年对生产工艺进行了改造（每半年为一个生产周期），从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示（如图）．已知每个生产周期内与其中位数误差在±5范围内（含±5）的产品为优质品，与中位数误差在±15范围内（含±15）的产品为合格品（不包括优质品），与中位数误差超过±15的产品为次品．企业生产一件优质品可获利润20元，生产一件合格品可获利润10元，生产一件次品要亏损10元（Ⅰ）求该企业2016年一年生产一件产品的利润为10的概率；
（Ⅱ）是否有95%的把握认为“优质品与生产工艺改造有关”．
附：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
7．函数f（x）=3-sinx-2cos2x，$x∈[{\frac{π}{6}，\frac{7π}{6}}]$，则函数的最大值与最小值之差为（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{7}{8}$ | D． | $\frac{9}{8}$ |
4．
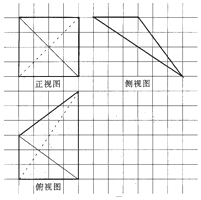如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）
如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）| A． | 4 | B． | 5 | C． | 4$\sqrt{2}$ | D． | $\sqrt{41}$ |
2．2016年8月江西某高校的成立了一个社会实践调查小组，在对大学生的“4G使用流量问题”的调查中，随机发放了120份问卷，对收回的100份有效问卷进行统计，得到如下2×2列联表：
（1）现已按4G使用流量问题采用分层抽样从45份男生问卷中抽取了9份问卷，试问应该从“流量超过1000M”和“流量没有超过1000M”各抽取多少人？
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| 流量超过1000M | 流量没有超过1000M | 合计 | |
| 男 | 20 | 25 | 45 |
| 女 | 40 | 15 | 55 |
| 合计 | 60 | 40 | 100 |
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |