题目内容
7.函数f(x)=3-sinx-2cos2x,$x∈[{\frac{π}{6},\frac{7π}{6}}]$,则函数的最大值与最小值之差为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{9}{8}$ |
分析 由已知得-$\frac{1}{2}$≤sinx≤1,利用同角平方关系对函数f(x)化简,结合二次函数的性质求出函数的最大、最小值.
解答 解:由正弦函数的性质可知,
当x∈[$\frac{π}{6}$,$\frac{7π}{6}$]时,sinx∈[-$\frac{1}{2}$,1];
∵函数f(x)=3-sinx-2cos2x
=2sin2x-sinx+1
=2${(sinx-\frac{1}{4})}^{2}$+$\frac{7}{8}$;
∴当sinx=$\frac{1}{4}$时,f(x)取得最小值为f(x)min=$\frac{7}{8}$;
当sinx=1或-$\frac{1}{2}$时,f(x)取得最大值为f(x)max=2;
∴函数的最大值与最小值之差为f(x)max-f(x)min=2-$\frac{7}{8}$=$\frac{9}{8}$.
故选:D.
点评 本题考查了正弦函数的性质以及利用配方法求二次函数的值域问题,要注意sinx的范围.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.如图所示是一个几何体的三视图,则这个几何体外接球的体积为( )
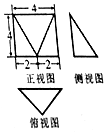

| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
18.某香料加工厂生产“沉鱼落雁”和“国色天香”两种香料,已知生产两种香料每吨所需的原材料A,B,C的数量和一周内可用资源数量如下表所示:
如果“沉鱼落雁”每吨的利润为400元,“国色天香”每吨的利润为300元,那么应如何安排生产,才能使香料加工厂每周的利润最大?并求出最大利润.
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
15.在平面直角坐标系中,“直线ax+y-1=0与直线x+ay+2=0平行”是“a=1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
2.当0<a<1时,函数y=loga(x2-4x+3)的单调增区间为( )
| A. | (-∞,2] | B. | [2,+∞) | C. | (-∞,1) | D. | (3,+∞) |
12.已知三条直线a、b、c两两平行且不共面,这三条直线可以确定m个平面,这m个平面把空间分成n个部分,则( )
| A. | m=2 n=2 | B. | m=2 n=6 | C. | m=3 n=7 | D. | m=3 n=8 |
19.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=x2+1 | B. | y=3-2x | C. | $y=\frac{1}{x}$ | D. | y=-x2+1 |
17.下列函数中是偶函数,且在(1,+∞)上是单调递减的函数为( )
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |