题目内容
4.不等式$\frac{1-x}{x+1}≤0$的解集是( )| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1] | D. | (-∞,-1)∪[1,+∞) |
分析 根据不等式的性质得到关于关于x的不等式组,解出即可.
解答 解:∵$\frac{1-x}{x+1}≤0$,即$\frac{x-1}{x+1}$≥0,
故$\left\{\begin{array}{l}{x-1≥0}\\{x+1>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-1≤0}\\{x+1<0}\end{array}\right.$,
解得:x≥1或x<-1,
故不等式的解集是(-∞,-1)∪[1,+∞),
故选:D.
点评 本题考查了解不等式问题,考查分类讨论思想,是一道基础题.

练习册系列答案
相关题目
12.某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.
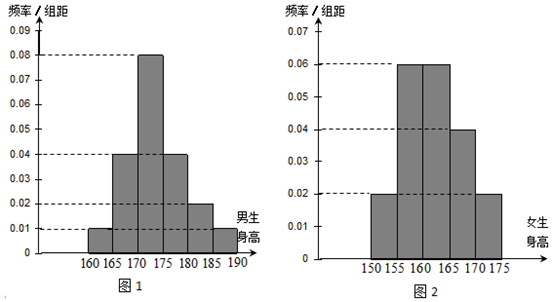
(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$

(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
19.已知命题p:f(x)=lnx+2x2+6mx+1在(0,+∞)上单调递增,q:m≥-5,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |