题目内容
已知点A（-3，2），B（1，-4），求AB线段的垂直平分线的方程．
考点：待定系数法求直线方程
专题：直线与圆
分析：设点P为线段AB的垂直平分线上的任意一点，则|PA|=|PB|，利用线段垂直平分线的性质、两点之间的距离公式即可得出．
解答：
解：设点P为线段AB的垂直平分线上的任意一点，则|PA|=|PB|，
∴
=
，
化为2x-3y-1=0．即为AB线段的垂直平分线的方程．
∴
| (x+3)2+(y-2)2 |
| (x-1)2+(y+4)2 |
化为2x-3y-1=0．即为AB线段的垂直平分线的方程．
点评：本题考查了线段垂直平分线的性质、两点之间的距离公式，属于基础题．
练习册系列答案
相关题目
在△ABC中，
=
，则B的值为（ ）
| cosC |
| cosB |
| 2a-c |
| b |
| A、30° | B、60° |
| C、90° | D、120° |
设f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+4）=f（x），且当x∈[-2，0]时，f(x)=(
)x-6
，若在区间（-2，6]内关于x的f（x）-loga（x+2）=0（a＞1）恰有3个不同的实数根，则a的取值范围是（ ）
| 1 |
| 3 |
，若在区间（-2，6]内关于x的f（x）-loga（x+2）=0（a＞1）恰有3个不同的实数根，则a的取值范围是（ ）
| A、（1，2） | |||
| B、（2，+∞） | |||
C、(1，
| |||
D、(
|
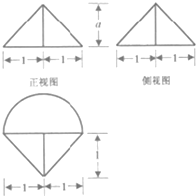一个几何体的三视图如图，其中正视图和侧视图是相同的等腰三角形，俯视图由半圆和一等腰三角形组成．则这个几何体可以看成是由