题目内容
设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=(
)x-6
,若在区间(-2,6]内关于x的f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| 1 |
| 3 |
,若在区间(-2,6]内关于x的f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| A、(1,2) | |||
| B、(2,+∞) | |||
C、(1,
| |||
D、(
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据指数函数的图象可画出:当x∈[-2,0]时,f(x)=(
)x-6的图象.根据偶函数的对称性质画出[0,2]的图象,再根据周期性:对任意x∈R,都有f(x+4)=f(x),画出[2,6]的图象.画出函数y=loga(x+2)(a>1)的图象.利用在区间(-2,6]内关于x的f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,即可得出.
| 1 |
| 3 |
解答:
解:如图所示,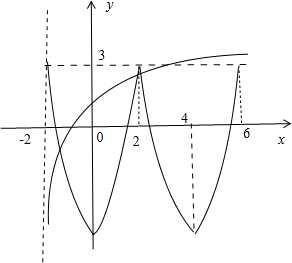
当x∈[-2,0]时,f(x)=(
)x-6,可得图象.
根据偶函数的对称性质画出[0,2]的图象,再根据周期性:对任意x∈R,都有f(x+4)=f(x),
画出[2,6]的图象.
画出函数y=loga(x+2)(a>1)的图象.
∵在区间(-2,6]内关于x的f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,
∴loga8>3,loga4<3,
∴4<a3<8,
解得
<a<2.
故选:D.

当x∈[-2,0]时,f(x)=(
| 1 |
| 3 |
根据偶函数的对称性质画出[0,2]的图象,再根据周期性:对任意x∈R,都有f(x+4)=f(x),
画出[2,6]的图象.
画出函数y=loga(x+2)(a>1)的图象.
∵在区间(-2,6]内关于x的f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,
∴loga8>3,loga4<3,
∴4<a3<8,
解得
| 3 | 4 |
故选:D.
点评:本题考查了指数函数的图象与性质、函数的奇偶性、周期性,考查了方程的实数根转化为函数图象的交点个数,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用数学归纳法证明:1+
+
+…+
<k+1(n∈N*),由n=k(k∈N*)不等式成立,推证n=k+1时,左边应增加的项数是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n |
| A、2k |
| B、2k-1 |
| C、2k+1 |
| D、2k-1 |
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |