题目内容
9.一个袋中装有3个红球和1个白球,现从袋中取出1球,然后放回袋中再取出一球,则两次取出的球颜色相同的概率是$\frac{5}{8}$.分析 两次取出的球颜色相同的对立事件是两次取出的球不同,由此利用对立事件概率计算公式能求出两次取出的球颜色相同的概率.
解答 解:一个袋中装有3个红球和1个白球,现从袋中取出1球,然后放回袋中再取出一球,
基本事件总数n=4×4=16,
两次取出的球颜色相同的对立事件是两次取出的球不同,
∴两次取出的球颜色相同的概率:
p=1-$\frac{3×1}{8}$=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
1.等差数列{an}中,a2+a3+a4=3,Sn为等差数列{an}的前n项和,则S5=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.设a=1111111(2),b=2001(4),c=242(7),则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
19.已知$\vec a,\vec b$均为单位向量,且$(2\vec a+\vec b)•(\vec a-2\vec b)=-\frac{{3\sqrt{3}}}{2}$,则向量$\vec a,\vec b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
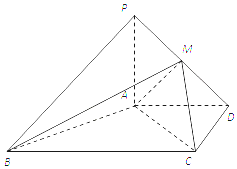 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,BC=4$\sqrt{2}$,PA=2,点M在PD上.