题目内容
18.已知正整数m的3次幂有如下分解规律:13=1;23=3+5;33=7+9+11; 43=13+15+17+19;…若m3(m∈N+)的分解中最小的数为91,则m的值为10.分析 由题意知,n的三次方就是n个连续奇数相加,且从2开始,这些三次方的分解正好是从奇数3开始连续出现,由此规律即可建立m3(m∈N*)的分解方法,从而求出m的值.
解答 解:由题意,从23到m3,正好用去从3开始的连续奇数共2+3+4+…+m=$\frac{(m+2)(m-1)}{2}$个,
91是从3开始的第45个奇数
当m=9时,从23到93,用去从3开始的连续奇数共$\frac{(9+2)(9-1)}{2}$=44个
当m=10时,从23到103,用去从3开始的连续奇数共$\frac{(10+2)(10-1)}{2}$=54个.
故m=10.
故答案为:10
点评 本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键.

练习册系列答案
相关题目
6.若直线y=3x与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有公共点,则双曲线的离心率的取值范围为( )
| A. | $(1,\sqrt{10})$ | B. | $(\sqrt{10},+∞)$ | C. | $({1,\sqrt{10}}]$ | D. | $[{\sqrt{10}}\right.,+∞)$ |
13.已知z1=1-3i,z2=3+i,其中i是虚数单位,则$\frac{{\overline{z_1}}}{z_2}$的虚部为( )
| A. | -1 | B. | $\frac{4}{5}$ | C. | -i | D. | $\frac{4}{5}i$ |
8.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,过F2的直线交双曲线右支于P,Q两点,且PQ⊥PF1,若$|PQ|=\frac{5}{12}|P{F_1}|$,则双曲线离心率e为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{37}}}{2}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{37}}}{5}$ |
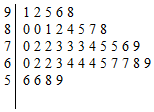 中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )
中国诗词大会的播出引发了全民的读书热,某小学语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如图所示.若规定得分不小于85分的学生得到“诗词达人”的称号,小于85分且不小于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号,根据该次比赛的成就按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )