题目内容
椭圆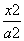 +
+ =1(a>b>0)与直线x+y-1=0相交于P,Q两点,且OP⊥OQ(O为原点).
=1(a>b>0)与直线x+y-1=0相交于P,Q两点,且OP⊥OQ(O为原点).
(1)求证: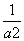 +
+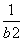 等于定值;
等于定值;
(2)若椭圆的离心率e∈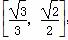 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.
(1)证明 由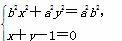 消去y,
消去y,
得(a2+b2)x2-2a2x+a2(1-b2)=0,①
∵直线与椭圆有两个交点,∴Δ>0,
即4a4-4(a2+b2)a2(1-b2)>0⇒a2b2(a2+b2-1)>0,
∵a>b>0,∴a2+b2>1.
设P(x1,y1),Q(x2,y2),则x1 、x2是方程①的两实根.
∴x1+x2=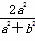 ,x1x2=
,x1x2=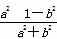 .②
.②
由OP⊥OQ得x1x2+y1y2=0,
又y1=1-x1,y2=1-x2,
得2x1x2-(x1+x2)+1=0.③
式②代入式③化简得a2+b2=2a2b2.④
∴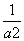 +
+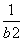 =2.
=2.
(2)解 利用(1)的结论,将a表示为e的函数
由e=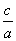 ⇒b2=a2-a2e2,
⇒b2=a2-a2e2,
代入式④,得2-e2-2a2(1-e2)=0.
∴a2= =
=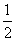 +
+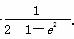 .
.
∵ ≤e≤
≤e≤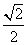 ,∴
,∴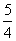 ≤a2≤
≤a2≤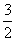 .
.
∵a>0,∴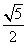 ≤a≤
≤a≤ .
.
∴长轴长的取值范围是[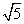 ,
,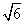 ].
].

练习册系列答案
相关题目
 x2或y=-
x2或y=- x2
x2 +
+ =1的右焦点重合,则p的值为( ).
=1的右焦点重合,则p的值为( ).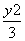 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则 的最小值为( ).
的最小值为( ). C.1 D.0
C.1 D.0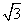 ,面积为3
,面积为3 和平面
和平面 ,则能推出
,则能推出 的是( )
的是( ) B.
B. 
 D.
D. 
 满足
满足
 的前
的前 项和
项和 .
.