题目内容
已知椭圆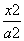 +
+ =1(a>b>0)的左、右焦点分别为F1和F2,由四个点M(-a,b)、N(a,b)、F2和F1组成了一个高为
=1(a>b>0)的左、右焦点分别为F1和F2,由四个点M(-a,b)、N(a,b)、F2和F1组成了一个高为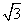 ,面积为3
,面积为3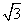 的等腰梯形.
的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A,B,求△F2AB面积的最大值.
解 (1)由条件,得b=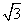 ,且
,且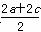 ×
×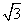 =3
=3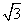 ,
,
所以a+c=3.又a2-c2=3,解得a=2,c=1.
所以椭圆的方程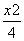 +
+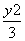 =1.
=1.
(2)显然,直线的斜率不能为0,设直线方程为x=my-1,直线与椭圆交于A(x1,y1),B(x2,y2).
联立方程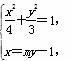 消去x,
消去x,
得(3m2+4)y2-6my-9=0,
因为直线过椭圆内的点,无论m为何值,直线和椭圆总相交.
∴y1+y2=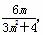 ,y1y2=-
,y1y2=-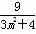 .
.
S△F2AB=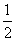 |F1F2||y1-y2|=|y1-y2|
|F1F2||y1-y2|=|y1-y2|
= 令t=m2+1≥1,设y=t+
令t=m2+1≥1,设y=t+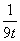 ,易知t∈
,易知t∈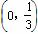 时,函数单调递减,t∈
时,函数单调递减,t∈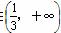 函数单调递增,所以当t=m2+1=1,即m=0时,ymin=
函数单调递增,所以当t=m2+1=1,即m=0时,ymin=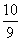 .
.
S△F2AB取最大值3.

练习册系列答案
相关题目
 -
-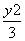 =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________. =1的焦点为F1,F2,点M在双曲线上且
=1的焦点为F1,F2,点M在双曲线上且 =0,则M到x轴的距离为________.
=0,则M到x轴的距离为________.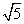 ) D.(1,
) D.(1,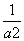 +
+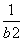 等于定值;
等于定值;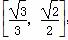 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围. 的值是 ( )
的值是 ( ) B.
B. C.
C. D. 2
D. 2
 ,在区间
,在区间 内任取两个实数
内任取两个实数 ,且
,且 ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为 B.
B.  C.
C.  D.
D. 
 ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 ≤0的解集为________.
≤0的解集为________.