题目内容
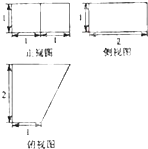
如图是一个几何体的三视图，根据图中数据，可得该几何体的体积是 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知：该几何体是直四棱柱，高为1，其底面是直角梯形，上下底长分别为1，2，梯形高为2．利用四棱柱的体积计算公式即可得出．
解答：
解：由三视图可知：该几何体是直四棱柱，高为1，其底面是直角梯形，上下底长分别为1，2，梯形高为2．
∴V=
×1=3．
故答案为：3．
∴V=
| 2×(1+2) |
| 2 |
故答案为：3．
点评：本题考查了由三视图恢复原几何体、四棱柱的体积计算公式，属于基础题．
练习册系列答案
相关题目
已知点A（0，1），点B在曲线C1：y=ex-1上，若线段AB与曲线C2：y=
相交且交点恰为线段AB的中点，则称点B为曲线C1与曲线C2的一个“相关点”，记曲线C1与曲线C2的“相关点”的个数为n，则（ ）
| 1 |
| x |
| A、n=0 | B、n=1 |
| C、n=2 | D、n＞2 |
定义在R上的函数f（x）对任意两个不相等的实数a，b，总有
＞0成立，则必有（ ）
| f(a)-f(b) |
| a-b |
| A、函数f（x）是先增加后减少 |
| B、f（x）在R上是增函数 |
| C、函数f（x）是先减少后增加 |
| D、f（x）在R上是减函数 |