题目内容
某生产车间甲、乙、丙三名工人生产了同一种产品,数量分别为240件、160件、120件,为了解他们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙的产品中抽取了6件,则n=( )
| A、18 | B、20 | C、24 | D、26 |
考点:分层抽样方法
专题:概率与统计
分析:根据分层抽样的定义,建立比例关系即可.
解答:
解:由分层抽样的定义可得:
=
,
解得n=26,
故选:D
| n |
| 240+160+120 |
| 6 |
| 120 |
解得n=26,
故选:D
点评:本题主要考查分层抽样的应用,根据条件建立比例关系是解决本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若x,y满足不等式
,则2x+y的最小值为( )
|
| A、-4 | B、3 | C、4 | D、0 |
函数y=f(x)满足:
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
| A、f(-1)>f(2) |
| B、f(-1)<f(2) |
| C、f(-1)=f(2) |
| D、无法确定 |
已知A={2,lnx},B={x,y},A∩B={1},则实数x,y的值分别为( )
| A、e,0 | ||
| B、e,1 | ||
| C、1,e | ||
D、
|
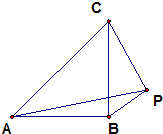 如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.
如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.