题目内容
已知点A(0,1),点B在曲线C1:y=ex-1上,若线段AB与曲线C2:y=
相交且交点恰为线段AB的中点,则称点B为曲线C1与曲线C2的一个“相关点”,记曲线C1与曲线C2的“相关点”的个数为n,则( )
| 1 |
| x |
| A、n=0 | B、n=1 |
| C、n=2 | D、n>2 |
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:设B(t,et-1),求出AB的中点为P,利用已知条件列出et=
,构造函数利用函数的图象的交点个数,判断方程解的个数,即可.
| 4 |
| t |
解答:
解:设B(t,et-1),则AB的中点为P(
,
),所以有
=
,即et=
,
所以“相关点”的个数就是方程ex=
解的个数,
由于y=ex的图象在x轴上方,且是R上增函数,
y=
在(0,+∞)上是减函数,
所以它们的图象只有一个交点,即n=1,
故选B.
| t |
| 2 |
| et |
| 2 |
| et |
| 2 |
| 2 |
| t |
| 4 |
| t |
所以“相关点”的个数就是方程ex=
| 4 |
| x |
由于y=ex的图象在x轴上方,且是R上增函数,
y=
| 4 |
| x |
所以它们的图象只有一个交点,即n=1,
故选B.
点评:本题考查函数与方程的综合应用,函数的零点,考查转化思想的应用.

练习册系列答案
相关题目
a,b∈R,记min{a,b}=
,函数f(x)=min{2-x2,x}(x∈R)的最大值( )
|
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
函数f(x)=log2|x|的图象( )
| A、关于直线y=-x对称 |
| B、关于原点对称 |
| C、关于y轴对称 |
| D、关于直线y=x对称 |
光线从点A(-3,5)射到x轴上,经反射以后经过点B(2,10),则光线从A到B的距离为( )
A、5
| ||
B、2
| ||
C、5
| ||
D、10
|
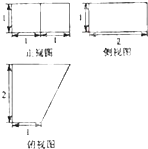
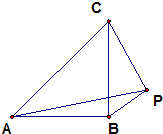 如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.
如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.