题目内容
若等比数列{an}的前n项和为Sn=3n-1，则其公比q为 ．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：利用等比数列的前n基和公式先求出a1，a2，由此能求出公比q．
解答：
解：∵等比数列{an}的前n项和为Sn=3n-1，
∴a1=S1=3-1=2，
a2=S2-S1=（32-1）-（3-1）=6，
∴公比q=
=
=3．
故答案为：3．
∴a1=S1=3-1=2，
a2=S2-S1=（32-1）-（3-1）=6，
∴公比q=
| a2 |
| a1 |
| 6 |
| 2 |
故答案为：3．
点评：本题考查等比数列的公比的求法，是基础题，解题时要认真审题，注意等比数列前n项和公式的合理运用．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
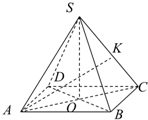如图，设S-ABCD是一个高为3的四棱锥，底面ABCD是边长为2的正方形，顶点S在底面上的射影是正方形ABCD的中心．K是棱SC的中点．试求直线AK与平面SBC所成角的大小．