题目内容
已知椭圆
+y2=1,直线x=t(t∈R)与椭圆相交于不同的两点A、B,若C(-3,0),D(3,0),直线CA与直线BD的交点K,则点K的轨迹方程为 .
| x2 |
| 9 |
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出A(t,y),B(t,-y),K(x,y),利用A在椭圆上有
+y2=1,求出CA,DB的方程,相乘,即可得到结论
| t2 |
| 9 |
解答:
解:依题意可设A(t,y),B(t,-y),K(x,y),且有
+y2=1
又CA:y=
(x+3),DB:y=
(x-3),
∴y2=
(x2-9),
将
+y2=1代入即得
-y2=1
∴点K的轨迹方程为
-y2=1.
故答案为:
-y2=1.
| t2 |
| 9 |
又CA:y=
| y |
| t+3 |
| -y |
| t-3 |
∴y2=
| -y2 |
| t2-9 |
将
| t2 |
| 9 |
| x2 |
| 9 |
∴点K的轨迹方程为
| x2 |
| 9 |
故答案为:
| x2 |
| 9 |
点评:本题考查椭圆的标准方程,考查方程与曲线的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
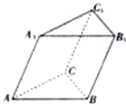 如图所示,在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2
如图所示,在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2