题目内容
已知函数f（x）=|x-1|+2|x+1|+1．
（Ⅰ）求不等式f（x）＜6的解集；
（Ⅱ）若直线y=（
）a（a∈R）与函数y=f（x）的图象恒有公共点，求实数a的取值区间．
（Ⅰ）求不等式f（x）＜6的解集；
（Ⅱ）若直线y=（
| 1 |
| 3 |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（Ⅰ）通过对自变量x取值范围的分类讨论，去掉不等式中的绝对值符号，解相应的不等式，最后取其并集即可；
（Ⅱ）由f(x)=
可求得函数f（x）的值域为[3，+∞），利用直线y=(
)a（a∈R）与函数y=f（x）的图象恒有公共点，即可求得实数a的取值区间．
（Ⅱ）由f(x)=
|
| 1 |
| 3 |
解答：
（本小题满分10分）选修4-5：不等式选讲
解：（1）因为f(x)=
…（3分）
所以当x＞1时，由f(x)＜6?3x+2＜6?x＜
，
又x＞1，所以1＜x＜
；
当-1≤x≤1时，f（x）＜6?x+4＜6?x＜2，
又-1≤x≤1，所以-1≤x≤1；
当x＜-1时，f（x）＜6?-3x＜6?x＞-2，
又x＜-1，所以-2＜x＜-1
综上，所求的解集为{x|-2＜x＜
}．…（6分）
（2）结合（1）知f(x)=
知，
当x＞1时，f（x）=3x+2＞5；
当-1≤x≤1时，f（x）=x+4∈[3，5]；
当x＜-1时，f（x）=-3x＞3；
∴函数f（x）的值域为[3，+∞）…（7分）
又直线y=(
)a（a∈R）与函数y=f（x）的图象恒有公共点，
所以(
)a≥3，∴a≤-1
即a的取值区间是（-∞，-1]．…（10分）
解：（1）因为f(x)=
|
所以当x＞1时，由f(x)＜6?3x+2＜6?x＜
| 4 |
| 3 |
又x＞1，所以1＜x＜
| 4 |
| 3 |
当-1≤x≤1时，f（x）＜6?x+4＜6?x＜2，
又-1≤x≤1，所以-1≤x≤1；
当x＜-1时，f（x）＜6?-3x＜6?x＞-2，
又x＜-1，所以-2＜x＜-1
综上，所求的解集为{x|-2＜x＜
| 4 |
| 3 |
（2）结合（1）知f(x)=
|
当x＞1时，f（x）=3x+2＞5；
当-1≤x≤1时，f（x）=x+4∈[3，5]；
当x＜-1时，f（x）=-3x＞3；
∴函数f（x）的值域为[3，+∞）…（7分）
又直线y=(
| 1 |
| 3 |
所以(
| 1 |
| 3 |
即a的取值区间是（-∞，-1]．…（10分）
点评：本题考查绝对值不等式的解法，着重考查分类讨论思想与综合运算能力，属于中档题．
练习册系列答案
相关题目
设a，b∈R，则“（a-b）3b2＞0”是“a＞b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
常说“便宜没好货”，这句话的意思是：“不便宜”是“好货”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
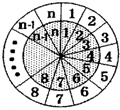如图所示的两个同心圆盘均被n等分（n∈N+且n≥2），在相重叠的扇形格中依次同时填上1，2，3，L，n，内圆盘可绕圆心旋转，每次可旋转一个扇形格，当内圆盘旋转到某一位置时，定义所有重叠扇形格中两数之积的和为此位置的“旋转和”．