题目内容
椭圆25x2+16y2=1的焦点坐标是 .
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:将椭圆的方程25x2+16y2=1为标准形式,可得a2=
,b2=
,即可求得答案.
| 1 |
| 16 |
| 1 |
| 25 |
解答:
解:椭圆的方程25x2+16y2=1化为标准形式为:
+
=1,
∴a2=
,b2=
,
∴c2=a2-b2=
,
又该椭圆焦点在y轴,
∴焦点坐标为:(0,
),(0,-
).
故答案为:(0,
),(0,-
).
| x2 | ||
|
| y2 | ||
|
∴a2=
| 1 |
| 16 |
| 1 |
| 25 |
∴c2=a2-b2=
| 9 |
| 400 |
又该椭圆焦点在y轴,
∴焦点坐标为:(0,
| 3 |
| 20 |
| 3 |
| 20 |
故答案为:(0,
| 3 |
| 20 |
| 3 |
| 20 |
点评:本题考查椭圆的简单性质,将椭圆的方程化为标准形式是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正四面体ABCD,线段AB∥平面α,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面α上的射影所成角余弦值的范围是( )
A、[0,
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
已知α为第二象限角,且sinα=
,则tanα的值为( )
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
将函数h(x)=2sin(2x+
)的图象向右平移
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象与函数h(x)的图象( )
| π |
| 4 |
| π |
| 4 |
| A、关于直线x=0对称 |
| B、关于直线x=1对称 |
| C、关于点(1,0)对称 |
| D、关于点(0,1)对称 |
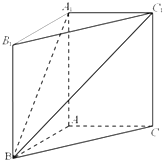 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB=