题目内容
若f(cosθ)=sin2θ-3sinθ,则f(2cos
)= .
| π |
| 3 |
考点:函数的值
专题:函数的性质及应用
分析:由f(2cos
)=f(cos0),利用已知条件能求出结果.
| π |
| 3 |
解答:
解:∵2cos
=1=cos0,f(cosθ)=sin2θ-3sinθ,
∴f(2cos
)=f(cos0)=sin20-3sin0=0.
故答案为:0.
| π |
| 3 |
∴f(2cos
| π |
| 3 |
故答案为:0.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意三角函数性质的灵活运用.

练习册系列答案
相关题目
正四面体ABCD,线段AB∥平面α,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面α上的射影所成角余弦值的范围是( )
A、[0,
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
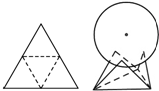 用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为
用一个边长为4的正三角形硬纸,沿各边中点连线垂直折起三个小三角形,做成一个蛋托,半径为1的鸡蛋(视为球体)放在其上(如图),则鸡蛋中心(球心)与蛋托底面的距离为