题目内容
5.已知以点A(m,$\frac{2}{m}$)(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.(1)当m=2时,求圆A的标准方程;
(2)当m变化时,△OBC的面积是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)设直线l:2x+y-4=0与圆A相交于P,Q两点,且|OP|=|OQ|,求|PQ|的值.
分析 (1)当m=2时,圆心A的坐标为(2,1),求出半径,即可求解圆的方程.
(2)∵圆A过原点O,求出圆A的方程,求出BC坐标,求出S△OBC,推出△OBC的面积为定值;
(3)∵|OP|=|OQ|,|AP|=|AQ|,说明OA垂直平分线段PQ,kPQ=-2,得到koA=$\frac{1}{2}$,求出m然后利用圆心到直线的距离与半径半弦长的关系求解即可.
解答 解:(1)当m=2时,圆心A的坐标为(2,1)
∵圆A过原点O,∴|OA|2=22+12=5
则圆A的方程是(x-2)2+(y-1)2=5;
(2)∵圆A过原点O,∴|OA|2=${m^2}+\frac{4}{m^2}$
则圆A的方程是(x-m)2+($y-\frac{2}{m}$)2=${m^2}+\frac{4}{m^2}$,
令x=0,得y1=0,y2=$\frac{4}{{{m^{\;}}}}$,∴$C({0,\frac{4}{m}})$
令y=0,得x1=0,x2=2m,∴B(2m,0)
∴S△OBC=$\frac{1}{2}|{OA}||{OB}|=\frac{1}{2}|{\frac{4}{m}}||{2m}|$=4,即:△OBC的面积为定值;
(3)∵|OP|=|OQ|,|AP|=|AQ|,∴OA垂直平分线段PQ,
∵kPQ=-2,∴koA=$\frac{1}{2}$,∴$\frac{{\frac{2}{m}}}{m}$=$\frac{1}{2}$,解得:m=2或m=-2,
∵已知m>0,∴m=2
∴圆A的方程为(x-2)2+(y-1)2=5.
此时A(2,1)到直线2x+y-4=0的距离d=$\frac{1}{\sqrt{5}}<\sqrt{5}$,
圆A与直线l:2x+y-4-0相交于两点,
|PQ|=$2\sqrt{{r^2}-{d^2}}$=$2\sqrt{5-\frac{1}{5}}$=$\frac{{4\sqrt{30}}}{5}$.
点评 本题考查直线与圆的方程的综合应用,考查转化思想以及计算能力.

 如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.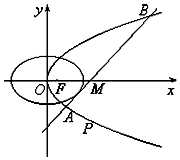 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.