题目内容
17．设A（-1，0），B是圆F：（x-1）2+y2=16上的动点，AB垂直平分线交BF于P，则动点P的轨迹方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1．分析 利用椭圆的定义判断点P的轨迹 是以A、F 为焦点的椭圆，求出a、b的值，即得椭圆的方程．
解答 解：由题意得 圆心F（1，0），半径等于4，|PA|=|PB|，
∴|PF|+|PA|=|PF|+|PB|=|BF|=半径4＞|AF|，
故点P的轨迹是以A、F 为焦点的椭圆，
2a=4，c=1，∴b=$\sqrt{3}$，
∴椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1．
故答案为：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1．
点评 本题考查用定义法求点的轨迹方程，结合椭圆的定义求轨迹是解题的难点．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
7．已知x∈（0，π），且cos（2x-$\frac{π}{2}$）=sin2x，则tan（x-$\frac{π}{4}$）等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
我们把离心率e=$\frac{\sqrt{5}+1}{2}$的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）称为黄金双曲线．如图是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0，c=$\sqrt{{a}^{2}+{b}^{2}}$）的图象，给出以下几个说法：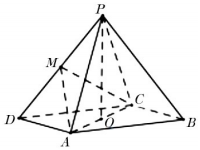
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ADC=45°，AD=AC=2，O为AC的中点，PO⊥平面ABCD且PO=6，M为BD的中点．