题目内容
10.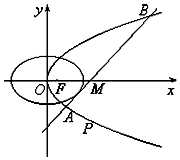 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.(1)求证:以AB为直径的圆过原点O;
(2)若坐标原点关于直线l的对称点P在抛物线C2上,直线l与椭圆C1相切,求椭圆C1的标准方程.
分析 (1)设出抛物线C2的标准方程,利用焦点F(1,0),即可得出结论;设AB:x=4+ny,代入抛物线方程,证明$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即可得出结论;
(2)P(4t2,4t),则OP⊥l,且OP的中点(2t2,2t)在直线l上,直线方程代入椭圆方程,利用△=0,可得结论.
解答  (1)解:抛物线C2的标准方程为:y2=2px,
(1)解:抛物线C2的标准方程为:y2=2px,
∵焦点F(1,0),
∴p=2
∴抛物线C2的标准方程为y2=4x;
设AB:x=4+ny,代入抛物线方程得y2-4ny-16=0,
设A(x1,y1),B(x2,y2),则y1y2=-16,x1x2=$\frac{{y}_{1}^{2}{y}_{2}^{2}}{16}$=16,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=0,
∴以AB为直径的圆过原点;
(2)解:设P(4t2,4t),则OP⊥l,且OP的中点(2t2,2t)在直线l上,
∴$\left\{\begin{array}{l}{2{t}^{2}=4+2nt}\\{\frac{4t}{4{t}^{2}}=n}\end{array}\right.$,∴n=±1,
由对称性,不妨设t<0,则n=1,直线l:x=y+4
设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{a}^{2}-1}$=1,a2>1,a>0,与直线x=y+4联立可得(2a2-1)y2+8(a2-1)y-a4+17a2-16=0,
由△=0得a2=$\frac{17}{2}$,b2=$\frac{15}{2}$,
∴椭圆方程为$\frac{2{x}^{2}}{17}$+$\frac{2{y}^{2}}{15}$=1
点评 本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 2ln 2 | B. | 2-ln 2 | C. | 4-ln 2 | D. | 4-2ln 2 |
| A. | 若a1<a2,则b1<b2,A的拟合效果更好 | |
| B. | 若a1<a2,则b1<b2,B的拟合效果更好 | |
| C. | 若a1<a2,则b1>b2,A的拟合效果更好 | |
| D. | 若a1<a2,则b1>b2,B的拟合效果更好 |
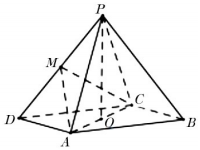 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=6,M为BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=6,M为BD的中点.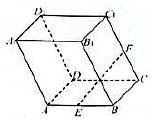 如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$.
如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$.