题目内容
已知函数f（x）=x+
，且其函数图象经过点（1，2）
（1）求实数a的值；
（2）判断函数在（0，a]和（1，+∞）的单调性，并说明理由．
| a |
| x |
（1）求实数a的值；
（2）判断函数在（0，a]和（1，+∞）的单调性，并说明理由．
考点：函数的图象,函数单调性的性质
专题：函数的性质及应用
分析：把点（1，2）的坐标代入f（x）=x+
，求出a．对函数f（x）求导，利用导数判断函数的单调性．
| a |
| x |
解答：
解：（1）∵函数f（x）=x+
，且其函数图象经过点（1，2），∴f（1）=2，
∴1+
=2，∴a=1．
（2）∵a=1，∴f(x)=x+
∴f′（x）=1-
=
=
，
令f′（x）=0得x=-1，或x=1
由f′（x）＞0得x＜-1或x＞1，由f′（x）＜0得-1＜x＜1，
∴在x∈（0，1]时f′（x）＜0，在x∈（1，+∞）时f′（x）＞0，
∴在f（x）在（0，1]上单调递增减，在（1，+∞）上单调递增．
| a |
| x |
∴1+
| a |
| 1 |
（2）∵a=1，∴f(x)=x+
| 1 |
| x |
∴f′（x）=1-
| 1 |
| x2 |
| x2-1 |
| x2 |
| (x+1)(x-1) |
| x2 |
令f′（x）=0得x=-1，或x=1
由f′（x）＞0得x＜-1或x＞1，由f′（x）＜0得-1＜x＜1，
∴在x∈（0，1]时f′（x）＜0，在x∈（1，+∞）时f′（x）＞0，
∴在f（x）在（0，1]上单调递增减，在（1，+∞）上单调递增．
点评：本题主要考查利用导数研究函数单调性，属于中档题．
练习册系列答案
相关题目
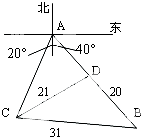观测站C处在目标A的南偏西20°方向，从A出发有一条南偏东40°走向的公路，在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去，走20km到达D处，此时测得CD距离21km，求此人在D处距A还有多远？定义在R上的函数f（x）满足f（x）=
，则f（2015）=（ ）
|
| A、-1 | B、0 | C、1 | D、2 |
函数f（x）=ln（x2+1）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
在△ABC中，角A、B、C的对边分别为a，b，c，a=1，b=
，∠A=
则∠B等于（ ）
| 3 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|