题目内容
设a=
dx,则二项式(ax-
)8的展开式中x2项的系数是( )
| ∫ | e e-1 |
| 1 |
| x |
| 1 | ||
|
| A、-1120 | B、1120 |
| C、-1792 | D、1792 |
考点:二项式定理的应用,定积分
专题:二项式定理
分析:先求定积分得到a=2,再求出二项式展开式的通项公式,再令x的幂指数等于2,求得r的值,即可求得展开式中x2项的系数.
解答:
解:∵a=
dx=lnx
=1-(-1)=2,则二项式(ax-
)8的展开式的通项公式为Tr+1=
•28-r•(-1)r•x8-
,
令8-
=2,求得 r=4,可得展开式中x2项的系数
•24=1120,
故选:B.
| ∫ | e e-1 |
| 1 |
| x |
| | | e e-1 |
| 1 | ||
|
| C | r 8 |
| 3r |
| 2 |
令8-
| 3r |
| 2 |
| C | 4 8 |
故选:B.
点评:本题主要考查求定积分,二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
已知a,b是实数,则“|a-b|=|a|-|b|”是“ab>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
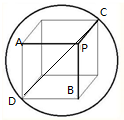 如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.
如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.