题目内容
19.已知向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,且$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,则k值为( )| A. | $\frac{7}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
分析 再利用向量坐标运算法则分别求出$\overrightarrow{a}+k\overrightarrow{b}$和2$\overrightarrow{b}$-$\overrightarrow{a}$,再由$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,可求出k.
解答 解:∵向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,
∴$\overrightarrow{a}+k\overrightarrow{b}$=(-1+k,k,2),2$\overrightarrow{b}$-$\overrightarrow{a}$=(3,2,-2),
∵$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,
∴($\overrightarrow{a}+k\overrightarrow{b}$)•(2$\overrightarrow{b}$-$\overrightarrow{a}$)=3(-1+k)+2k-4=0,
解得k=$\frac{7}{5}$.
故选:A.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意空间向量垂直的性质及坐标运算法则的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设O是坐标原点,若直线l:y=x+b(b>0)与圆x2+y2=4交于不同的两点P1、P2,且$|{\overrightarrow{{P_1}{P_2}}}|≥|{\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}}|$,则实数b的最大值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
4.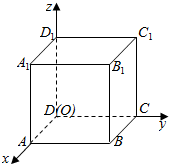 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是( )
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是( )
 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是( )
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是( )| A. | (2,-2,2) | B. | (-2,-2,2) | C. | (-2,2,2) | D. | (-2,-2,-2) |
11.函数$y={x^2}+\frac{1}{x}+1$在x=1处的切线方程是( )
| A. | x-y+2=0 | B. | x-y-4=0 | C. | x+y-4=0 | D. | x+y+2=0 |
8.若角α=2rad(rad为弧度制单位),则下列说法错误的是( )
| A. | 角α为第二象限角 | B. | α=$\frac{360°}{π}$ | C. | sinα>0 | D. | sinα<cosα |