题目内容
9.若0<y≤x<$\frac{π}{2}$且tanx=3tany,则x-y的最大值为$\frac{π}{6}$.分析 要使x-y最大,只需tan(x-y)最大,利用基本不等式求得tan(x-y)的最大值,可得x-y的最大值.
解答 解:∵0<y≤x<$\frac{π}{2}$且tanx=3tany,∴0≤x-y<$\frac{π}{2}$,要使x-y最大,只需tan(x-y)最大.
又tan(x-y)=$\frac{tanx-tany}{1+tanxtany}$=$\frac{2tany}{1+{3tan}^{2}y}$=$\frac{2}{\frac{1}{tany}+3tany}$≤$\frac{\sqrt{3}}{3}$,当且仅当tany=$\frac{\sqrt{3}}{3}$时,等号成立,
此时,y=$\frac{π}{6}$,tanx=$\sqrt{3}$,x=$\frac{π}{3}$,故x-y的最大值为$\frac{π}{3}$-$\frac{π}{6}$=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题主要考查基本不等式的应用,特殊角的三角函数值,属于基础题.

练习册系列答案
相关题目
19.已知向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,且$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,则k值为( )
| A. | $\frac{7}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
20.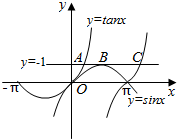 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
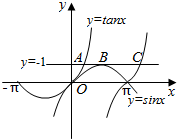 如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )
如图,已知A,B,C为直线y=1与函数y=sinx,y=tanx的图象在第一象限的三个相邻交点,若线段AC的长度记为|AC|,则|AB|:|BC|=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
17.若不等式a|x|>x2-$\frac{1}{2}$对任意x∈[-1,1]都成立,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,1)∪(1,2) | D. | (0,$\frac{1}{2}$)∪(1,2) |
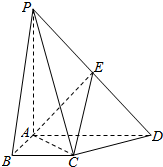 四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.
四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90°,PA⊥底面ABCD,PA=AD=2,BC=AB=1,E为PD的中点.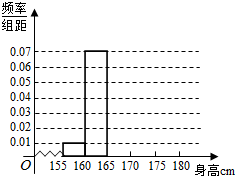 某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.
某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.