题目内容
7.设O是坐标原点,若直线l:y=x+b(b>0)与圆x2+y2=4交于不同的两点P1、P2,且$|{\overrightarrow{{P_1}{P_2}}}|≥|{\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}}|$,则实数b的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
分析 设P1P2中点为D,则OD⊥P1P2,确定|$\overrightarrow{OD}$|2≤2,即可求出实数b的最大值.
解答 解:设P1P2中点为D,则OD⊥P1P2,
∵$|{\overrightarrow{{P_1}{P_2}}}|≥|{\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}}|$,
∴|$\overrightarrow{{P}_{1}{P}_{2}}$|≥2|$\overrightarrow{OD}$|,
∵|$\overrightarrow{OD}$|2+$\frac{1}{4}$|$\overrightarrow{{P}_{1}{P}_{2}}$|2=4
∴|$\overrightarrow{OD}$|2≤2
∵直线l:y=x+b(b>0)与圆x2+y2=4交于不同的两点P1、P2,
∴|$\overrightarrow{OD}$|2<4
∴|$\overrightarrow{OD}$|2≤2
∴($\frac{|b|}{\sqrt{2}}$)2≤2
∵b>0
∴b≤2.
∴实数b的最大值是2.
故选:B.
点评 本题考查直线与圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
12.已知x∈(0,2π),函数y=$\sqrt{sinx}$+$\sqrt{-cosx}$的定义域是( )
| A. | [0,π] | B. | [$\frac{π}{2}$,$\frac{3π}{2}$] | C. | [$\frac{π}{2}$,π] | D. | [$\frac{3π}{2}$,2π] |
13.已知函数f(x)=ax2+bx+c的图象在点x=1处的切线l为直线3x-y-1=0,Tn=f(n)为等差数列{an}的前n项和,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S2015的值为( )
| A. | $\frac{2010}{2011}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2017}{2018}$ |
15.参数方程$\left\{\begin{array}{l}{x=t-1}\\{y={t}^{2}+2}\end{array}\right.$(t∈R)表示的曲线是( )
| A. | 经过坐标原点 | B. | 与x轴相交,但与y轴不相交 | ||
| C. | 与y轴相交,但与x轴不相交 | D. | 不经过坐标原点,但与x轴、y轴相交 |
2.圆(x-2)2+y2=4被直线x=1截得的弦长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
19.已知向量$\overrightarrow a=(-1,0,2),\overrightarrow b=(1,1,0)$,且$\overrightarrow a+k\overrightarrow b与2\overrightarrow b-\overrightarrow a$相互垂直,则k值为( )
| A. | $\frac{7}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | 1 |
16.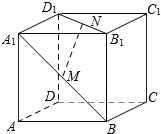 如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
 如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )
如图,在正方体ABCD-A1B1C1D1中,点M,N分别是面对角线A1B与B1D1的中点,若$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}$($\overrightarrow{c}$+$\overrightarrow{b}$-$\overrightarrow{a}$) | B. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\frac{1}{2}$($\overrightarrow{a}$-$\overrightarrow{c}$) | D. | $\frac{1}{2}$($\overrightarrow{c}$-$\overrightarrow{a}$) |
17.若不等式a|x|>x2-$\frac{1}{2}$对任意x∈[-1,1]都成立,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,1)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,1)∪(1,2) | D. | (0,$\frac{1}{2}$)∪(1,2) |