题目内容
20.已知{an}是等比数列,a1=1,a2=2,则a1a2+a2a3+…+anan+1=( )| A. | $\frac{2}{3}$(1-4-n) | B. | $\frac{2}{3}$(1-2-n) | C. | $\frac{2}{3}$(4n-1) | D. | 2n+1-2 |
分析 由题意易得{anan+1}是首项为2,公比为4的等比数列,由等比数列的求和公式可得.
解答 解:∵{an}是等比数列,∴{anan+1}也是等比数列,
又a1=1,a2=2,∴a3=4,∴a1a2=2,a2a3=8,
∴{anan+1}是首项为2,公比为$\frac{8}{2}$=4的等比数列,
∴a1a2+a2a3+…+anan+1=$\frac{2(1-{4}^{n})}{1-4}$=$\frac{2}{3}$(4n-1),
故选:C.
点评 本题考查等比数列的通项公式和求和公式,涉及等比数列的判定,属基础题.

练习册系列答案
相关题目
11.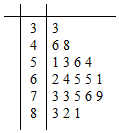 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
(Ⅱ) 根据列联表数据判断:能否在犯错的概率不超过5%的前提下,认为“满意与否”与“性别”有关?
附:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
附:
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
15.若等差数列{an}满足a8+a9+a10>0,a9+a10<0,则当n=( )时,{an}的前n项和最大.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
12.已知具有线性相关的两个变量x,y之间的一组数据如表:
且回归方程是$\stackrel{∧}{y}$=0.95x+2.6,则t=( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 2.5 | B. | 3.5 | C. | 4.5 | D. | 5.5 |
9.设i为虚数单位,则复数$\frac{1-i}{i}$的共轭复数所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
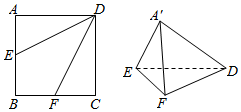 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′. 如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.
如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.