题目内容
11.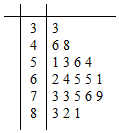 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
附:
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
分析 (Ⅰ)根据茎叶图中的数据,填写2×2列联表,计算所求的概率值;
(Ⅱ) 根据列联表中的数据,计算K2,对照数表得出结论;
(Ⅲ)利用列举法求出基本事件数,计算对应的概率值即可.
解答 解:(Ⅰ)根据茎叶图中的数据,填写2×2列联表如下,
又样本容量是20,对该公司产品满意的有6人,
所以估计用户对该公司的产品“满意”的概率为P=$\frac{6}{20}$=0.3;
| 不满意 | 满意 | 合计 | |
| 男 | 3 | 4 | 7 |
| 女 | 11 | 2 | 13 |
| 合计 | 14 | 6 | 20 |
所以在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关;
(Ⅲ)由(Ⅰ)知,对该公司产品满意的用户有6人,其中男用户4人,女用户2人;
设男用户分别为a、b、c、d,女用户分别为E、F,
从中选取2人,记事件A为“选取的两人都是男用户或都是女用户”,则总的基本事件为
ab、ac、ad、aE、aF、bc、bd、bE、bF、cd、cE、cF、dE、dF、EF共15个,
而事件A包含的基本事件为
ab、ac、ad、bc、bd、cd、EF共7个,
故所求的概率为P(A)=$\frac{7}{15}$.
点评 本题考查了茎叶图以及独立性检验的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
2.曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
19.已知f(x)=sin(x+$\frac{π}{6}$),若sinα=$\frac{3}{5}$(0<α<$\frac{π}{2}}$),则f(α+$\frac{π}{12}}$)=( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
20.已知{an}是等比数列,a1=1,a2=2,则a1a2+a2a3+…+anan+1=( )
| A. | $\frac{2}{3}$(1-4-n) | B. | $\frac{2}{3}$(1-2-n) | C. | $\frac{2}{3}$(4n-1) | D. | 2n+1-2 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点