题目内容
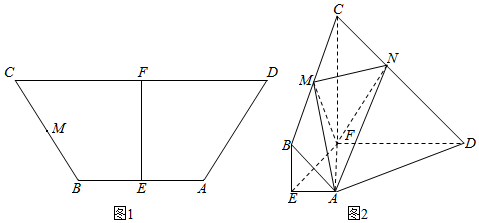
10.如图1,在等腰梯形ABCD中,AB∥CD,E,F分别为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点,现将梯形BEFC沿EF所在直线折起,使平面EFCB⊥平面EFDA,如图2所示,N是CD上一点,且$CN=\frac{1}{2}ND$.(Ⅰ)求证:MN∥平面ADFE;
(Ⅱ)求三棱锥F-AMN的体积.
分析 (I)取EF的中点P,连结MP,过点N作NQ∥CF交DF于点Q,连接PQ.利用中位线定理得出四边形MPQN是平行四边形,故MN∥PQ,于是MN∥平面ADFE;
(II)延长DA,FE,CB交于一点H,利用平行线等分线段成比例得出MN与DH的比值,得出△AMN与△CDH的面积比,则三棱锥F-AMN与三棱锥F-CDH的体积比等于其底面积的比.
解答 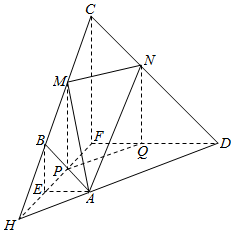 解:(Ⅰ)取EF的中点P,连结MP,过点N作NQ∥CF交DF于点Q,连接PQ.
解:(Ⅰ)取EF的中点P,连结MP,过点N作NQ∥CF交DF于点Q,连接PQ.
则MP∥CE,$MP=\frac{BE+CF}{2}=2$.
$\frac{NQ}{CE}=\frac{DN}{CD}=\frac{2}{3}$,∴NQ=2,
∴MP$\stackrel{∥}{=}$NQ,
∴四边形MPQN是平行四边形
∴MN∥PQ,又PQ?平面ADFE,MN?平面ADFE,
∴MN∥平面ADFE.
(Ⅱ)延长DA,FE,CB交于一点H,
∵$\frac{BE}{BF}=\frac{AE}{DF}=\frac{1}{3}$,∴BE=$\frac{1}{2}EF=1$,
∴$\frac{FP}{FH}=\frac{1}{3}$,∵$\frac{FQ}{FD}=\frac{CN}{CD}=\frac{1}{3}$,∴PQ∥DH,且$\frac{PQ}{DH}=\frac{1}{3}$.
∵MN=PQ,MN∥PQ,∴MN$\stackrel{∥}{=}\frac{1}{3}DH$.
∴$\frac{{S}_{△MNA}}{{S}_{△CDH}}$=$\frac{2}{9}$,∴$\frac{{V}_{F-AMN}}{{V}_{F-CDH}}=\frac{2}{9}$.
∵${V_{F-CDH}}={V_{C-FDH}}=\frac{1}{3}×3×\frac{1}{2}×3×3=\frac{9}{2}$,
∴VF-AMN=1.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
| A. | $\frac{2}{3}$(1-4-n) | B. | $\frac{2}{3}$(1-2-n) | C. | $\frac{2}{3}$(4n-1) | D. | 2n+1-2 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点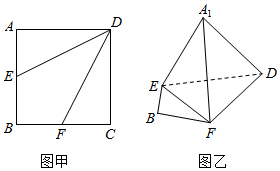
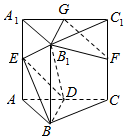 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点. 如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.