题目内容
若不等式(-1)n•a<3+
对任意自然数n恒成立,则实数a的取值范围是 .
| (-1)n+1 |
| n+1 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式进行参数分离,求函数的最值即可得到结论.
解答:
解:当n为奇数时,不等式可化为-a<3+
,即a>-3-
,
要使不等式对任意自然数n恒成立,则a≥-3;
当n为偶数时,不等式可化为a<3-
,
要使不等式对任意自然数n恒成立,
则a<(3-
)min?=3-1=2,
即a<2.
综上:-3≤a<2.
故答案为:[-3,2).
| 1 |
| n+1 |
| 1 |
| n+1 |
要使不等式对任意自然数n恒成立,则a≥-3;
当n为偶数时,不等式可化为a<3-
| 1 |
| n+1 |
要使不等式对任意自然数n恒成立,
则a<(3-
| 1 |
| n+1 |
即a<2.
综上:-3≤a<2.
故答案为:[-3,2).
点评:本题主要考查不等式恒成立问题,将不等式恒成立转化为求式子的最值是解决恒成立问题的基本方法.

练习册系列答案
相关题目
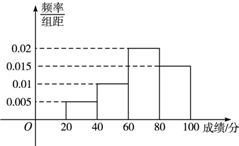 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )| A、63 | B、65 | C、68 | D、70 |
已知全集U={0,1,2,3,4},集合A={1,2},B={2,3,4},则B∩∁UA的子集个数有( )
| A、2 | B、4 | C、8 | D、16 |
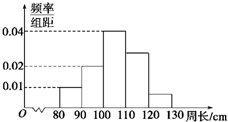 为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )| A、3000 | B、6000 |
| C、7000 | D、8000 |
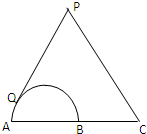 如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若
如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若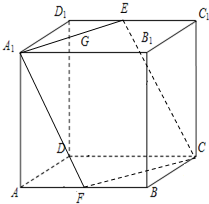 如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为
如图,在正方体ABCD-A1B1C1D1中,E、F分别为C1D1与AB的中点,则A1B1与截面A1ECF所成角的大小为